4ª avaliação de Aspectos Teóricos da Computação

4ª avaliação da disciplina EXA858 – Aspectos Teóricos da Computação.
Valor: 10,0 na 3ª unidade.
Prazo: 15/05/2016, 23:59 (via e-mail).
Em dupla.

Crie um programa que implemente uma máquina de Turing descrita em arquivo. O arquivo terá o formato abaixo:

alfabeto
número de transições
transição1
transição2
...

Os itens do alfabeto devem ser separados por espaço. O estado inicial é o primeiro estado a aparecer na lista de transições. O número de transições é um inteiro e cada transição deve estar na forma:

qi,fi,qj,fo,M

• qi = estado atual
• fi = caractere lido da fita
• qj = próximo estado
• fo = caractere gravado na fita
• M = movimento da fita, que pode ser S (fique onde está), L (esquerda) ou R (direita)

Os ítens da transição estão separados por vírgula para facilitar a inserção de espaços em branco na fita, além de que a inserção de elementos na fita é opcional e pode ser omitita. O estado de aceitação deve se chamar sempre ‘qA’ e o de rejeição é ‘qR’. Exemplo de arquivo:

0
15
q0, ,qR,,R
q0,x,qR,,R
q0,0,q1, ,R
q1, ,qA,,R
q1,x,q1,,R
q1,0,q2,x,R
q2,x,q2,,R
q2,0,q3,,R
q2, ,q4,,L
q3, ,qR,,R
q3,x,q3,,R
q3,0,q2,x,R
q4,0,q4,,L
q4,x,q4,,L
q4, ,q1,,R

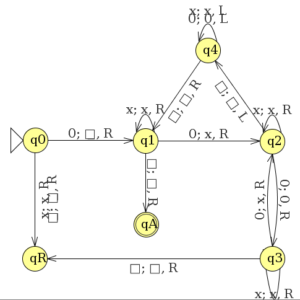
O exemplo acima implementa a máquina de Turing que decide A = {0^2^n | n >= 0} (veja a imagem abaixo). Após ler o arquivo, o programa deverá solicitar uma string ao usuário, essa string será a fita da máquina. Em seguida, o programa deverá informar se a string na fita é aceita ou rejeitada pela máquina.